TonyWilliams
Well-known member
Previous Planning for Sept 15, 2012 Phoenix Range Test
Subsequent 2013 LEAF-S Range Test on Feb 22, 2013
Subsequent 2012 & 2013 LEAF-SL Range Test, San Diego, March 8, 2013
Nissan LEAF Range Autonomy Demonstration
With Reduced Battery Capacity
September 18, 2012
by
Tony Williams
San Diego, California USA
[email protected]
The Nissan LEAF electric car was introduced to the world as a mass production vehicle during December 2010. Almost 40,000 have been sold around the world in the short time since then, with well over 10,000 sold in the USA. Unfortunately, a percentage of those USA cars that are operated in hot climates, such as Phoenix, Arizona, and the state of Texas, have experienced accelerated losses of the vehicle’s range autonomy, when compared to its performance when new. The phenomenon is not relegated solely to areas of extreme heat; many LEAFs now in moderate temperature areas of California have also experienced significant range autonomy reduction, however not yet to the extent of those cars exposed to Arizona and Texas heat.
When customers have complained, thus far Nissan has claimed that any reduction in range is “normal”, regardless of how much that capacity loss is. Battery issues that are covered under the warranty include “power” to accelerate, or a specific battery failure or abrupt change in the battery performance. Nissan specifically claims that they do not warranty capacity. Nonetheless, in late 2011, Nissan did exchange at least one battery of an Arizona LEAF when its owner complained of reduced capacity. That replacement battery also began degrading recently, and the owner subsequently relinquished the car as a result.
In July 2012, with increasing numbers of LEAFs reporting battery capacity problems, Nissan took approximately one half dozen Phoenix area LEAFs whose owners had complained of reduced range and lowered battery capacity (as indicated by the vehicle’s dash mounted instrument) to its corporate testing facility in Casa Grande, Arizona.
All of those cars have since been returned to their owners, however none of those returned cars had reported any positive change in actual performance by their owners. One car’s battery capacity instrument was reset by Nissan to a “like new” battery indication of 12 of 12 instrument segments, from its previous 10 or 12 segments (10 segments indicates 72.5% - 78.74% battery capacity per Nissan documents). This same car once again lost the 12th capacity segment (with 11 of 12 remaining) on Sunday, September 16, 2012. Of the cars sent to Casa Grande, none have been reported to have been driven by Nissan more than a few dozen miles while at the testing facility.
One prominent Nissan executive is frequently quoted saying that the LEAF should have 80% capacity in 5 years, and 70% capacity in 10 years, and in fact, he specifically states during a Nissan produced YouTube video that those figures are considered “gradual” loss of capacity. Earlier this month, an Australian news agency reported that a Nissan Executive Vice President with specific experience with the LEAF, Mr. Andy Palmer, said that there is “no problem” with the LEAF battery, and that the any customer complaints were merely the result of instrument problems.
In response to this revelation, a group of twelve Nissan LEAFs were independently gathered on Saturday, September 15, 2012 in Phoenix to put this statement to an actual range test; driving a fully charged LEAF in controlled conditions to measure how far they could actually go. Any battery test (or allegation of good batteries) is meaningless if the car can’t actually do the job it was designed to do. In the USA, that job is advertised as traveling “100 miles” (161km), and even further, 200 kilometers (124 miles) in Japan. Clearly, if Nissan truly felt that the batteries were performing as designed for the customer cars they tested at Casa Grande in July, they could have simply verified that at the private, purpose built test track at their disposal there. The actual driving portion of the test would have taken about 90 minutes per car, but they chose not to. Four of the twelve cars in Saturday’s Phoenix area test were previously at the Casa Grande test facility in July.
A staging area was selected at 7755 South Research Drive, Tempe, Arizona, which has one DC Chademo fast charger, and two J1772-2009 EVSE charging stations. Equipment was used to split the latter two stations into four total EVSE’s. This staging site was conveniently located within 0.3 miles (0.5 km) from the main highway. The route traveled was highway 101 north for 5.2 miles (8.3 km), then highway 202 west which becomes highway 10 west. Each car continued west until a predetermined course reversal point, and then returned to near the starting point. This route is largely level and with dry asphalt or concrete roadbed in excellent condition.
Turn around points were determined based on predicted range of each car after considering each car’s battery capacity meter and viewing the car’s report of stored watt-hours with additional equipment. The following round trip distances apply at these course reversal exits on highway 10. The total distance measured is from the staging area and ending on the 101 highway southbound at the East Elliot Road overpass at highway 101. The percentages are the battery’s stored available energy:
62% - 52.3 miles (83.7 km) - Exit 136, 75th Avenue
64% - 54.3 miles (87.4 km) - Exit 135, 83rd Avenue
67% - 56.3 miles (90.6 km) - Exit 134, 91st Avenue
69% - 58.3 miles (93.8 km) - Exit 133a, 99th Avenue
74% - 62.3 miles (100.3km) - Exit 131, 115th Ave / Avondale Boulevard
79% - 66.3 miles (106.7km) - Exit 129, Dysart Road
81% - 68.3 miles (109.9km) - Exit 128, Litchfield Road
85% - 72.3 miles (116.4km) - Exit 126, Pebble Beach Parkway / Estrella Parkway
91% - 76.3 miles (122.8km) - Exit 124, Cotton Lane / highway 303
98% - 82.3 miles (132.5km) - Exit 121, 195th Avenue / Jackrabbit Trail
101%- 85.1 miles (136.9km) - Exit 120, Airport Road / Verrado Way
109%- 91.5 miles (153.0km) - Exit 117, Watson Road
The dash display of Battery Capacities per Nissan documents are as follows:
53.75% - 59.99% - 7 segments of 12 illuminated
60.00% - 66.24% - 8 segments of 12 illuminated
66.25% - 72.49% - 9 segments of 12 illuminated
72.50% - 78.74% - 10 segments of 12 illuminated
78.75% - 84.99% - 11 segments of 12 illuminated
85.00% - 100.0% - 12 segments of 12 illuminated
The backup routes, in case of highway closures, crashes, etc., were either a 40.4 mile (64.6 km) “RIGHT LOOP” consisting of highway 101 North, 60 East, 202 South and then West, then 101 North again, or a 21.8 mile (34.9 km) “LEFT LOOP” via 101 North, 60 West, 10 South, 202 East and returning to 101 North. None of the cars took either of these latter routes. The only highway closure was Cotton Lane exit on highway 10.
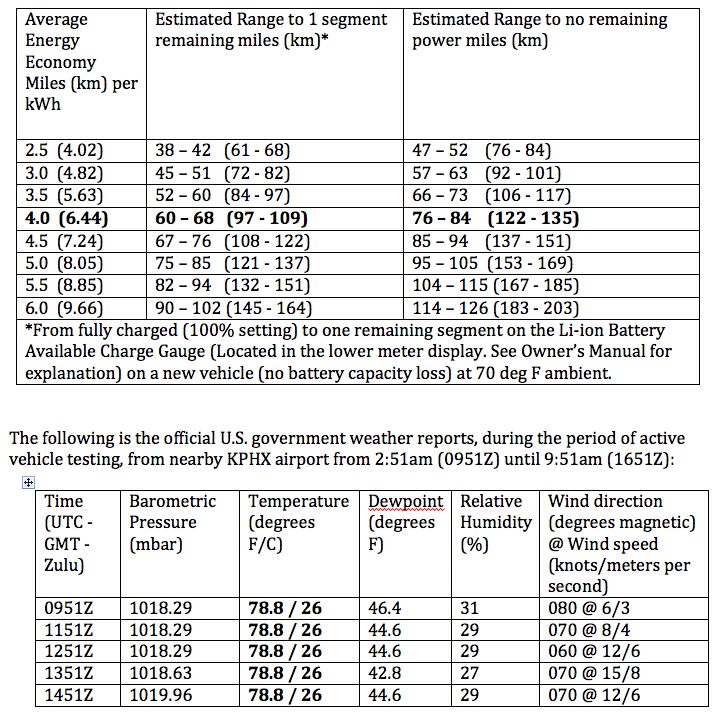
The course was driven at 100 km/h as measured by the LEAF’s onboard GPS (62 mph ground speed, 64 mph indicated speed as displayed on the LEAF’s speedometer) with the cruise control engaged. It was estimated that this speed would yield a target energy usage rate of 4 miles (6.437 km) per kWh without climate control. Based on Nissan’s published official range data below (from Nissan Technical Bulletin NTB11-076a), it was determined that a new car would travel 84 miles (135 km) until “turtle” mode (a reduced power mode to safely get the vehicle off the road before the battery disengages power altogether). This data is consistent with extensive publically available independent testing.
Air Density Calculation
Elevation: 1135 feet (346 meters)
Air Temperature: 80F (26.6C)
Altimeter Setting: 30.09 inches Hg (1018.5 hPa)
Dew Point: 43F (6C)
Density Altitude: 2685 feet (819 meters)
Absolute Pressure: 28.864 inches Hg (977.46 hPa)
Air Density: 0.0706 lb/ft3 (1.132 kg/m3)
Relative Density: 92.38%
All LEAFs in this test had the front bumper tow hook installed. All trip odometers, miles/kWh, average speed, timers, etc., were reset. Headlights were on, climate control off and tires set to 36 pounds per square inch (2.48 bars) pressure. All assigned routes were programmed into each navigation display.
Each car had a stored energy display meter (Gidmeter) installed. A new LEAF in optimum condition will show 281 units reported by the LEAF’s automation, for a total of 281 x 80 watt hours per unit = 22.48 kWh stored in the battery. This value, referred to in the LEAF community as “Gids”, is alternately displayed as a percentage of 281 (281 would equal 100%). The LEAF battery has an advertised capacity of 24 kWh.
To help keep track of each of the cars, the last three digits of the LEAF's serial number were affixed on the right top front of the windshield and left rear top of the rear window. Stickers were added to the dash to remind the drivers not to use climate control (or even turn the fan on, as that powers the climate control) and for other safety related functions. Lighter weight driver’s cars had ballast added to match heaviest drivers. The front windows could be either closed, or up to 2 inches open. Rear windows were not to be opened. Most drivers were not the owner of the car they drove, but instead drove another car. Every car was charged the night before, and left outside to be exposed to ambient air for a minimum of 4 hours (most cars well exceeded this). A secondary goal to this was to allow time for the LEAF’s automation to properly balance the 96 cell pairs.
At the start of each car’s test, the driver recorded the starting position GPS coordinates, time from the GPS clock, battery pack voltage (typically 393.5), the “Gid” percentage, Fuel segments observed (in every case, 12), battery capacity segments (varied from 8 to 12, depending on which car) and battery temperature segments displayed (6 in every case, indicating temperatures between approximately 50F (10C) to 100F (38C) per Nissan documents).
Each car had a nine page comprehensive checklist and information package. Finally, the “Distance to Empty” meter readout was recorded. This is largely for entertainment value, as the meters are known to provide such wide variations from actual expected performance that it is affectionately known as the “Guess… Oh… meter”, or “GOM” amongst LEAF owners.
At the conclusion of each run, after the car was safely off the road, and awaiting one of five recovery vehicles used (four rental car dollies attached to gasoline tow vehicles, and one flatbed truck), GPS coordinates were once again recorded, the time from the GPS clock, battery pack voltage, Gid percent, fuel bar segments illuminated, battery capacity segments illuminated and temperature segments illuminated. Finally, the trip odometer mileage and the dash readout of miles/kWh were recorded.
Following is the performance of each car:
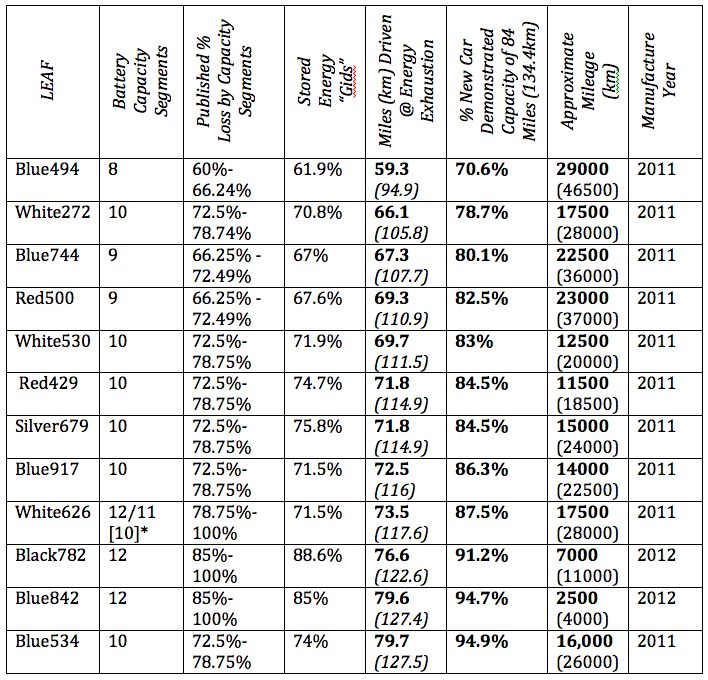
*White626 had previous lost one, then two capacity segments. Then, the car was sent to Nissan's test facility at Casa Grande and when it was returned, all 12 capacity segments were restored. One day after this test, it once again lost one capacity segment, now down to 11.
Conclusions and Opinions
The Nissan LEAF has only been on the world stage for about 21 months. Many in the automotive battery world expressed concern over Nissan deploying this chemistry in hot climates without a means to regulate battery temperature long before a single LEAF was built. Only LEAFs in very stable and mostly cool places like England, the San Francisco peninsula, Seattle, Portland (which this summer had unseasonably cooler temperatures, while the rest of the USA baked) have been largely immune from degradation. Even San Diego, where I live, has reported cases of battery degradation.
Both of the 2012 cars (my car was one of them) in the test were replacements for previous LEAFs that suffered battery degradation. Nissan offered no assistance or consideration for the previous cars shortcomings for these new leases. Battery reports issued by the dealers were consistently “5 of 5” stars.
One of the many challenges in this endeavor was finding a “control” car that could actually test out at 100% battery capacity. LEAFs sitting on dealer’s lots in Phoenix, and other hot places, usually with very high states of charge, are in a very difficult situation for the long life of the battery. None of the cars in our group could even come close to 100%, and that includes both of the 2012 model cars, both of which were built in April 2012; one with 2500 and the other 7000 miles.
I planned, and completed a promotional trip from Mexico to Canada, “BC2BC”, in June 2012 with my Nissan LEAF. However, my first car could not complete the trip as planned, due to its reduced range capability, so I leased my current LEAF, built in April 2012 and took delivery at the end of May. Now, with 7000 miles (11000 km), and only 3 months of actual use, this car could not complete the trip that it did in June. During the BC2BC trip, several times I arrived with 4%-5% capacity remaining, which means today, just a few months later, I would come up 4%-5% short. This car has never been exposed to the heat of Phoenix, although it was 104F (40C) in San Jose, California the one day that I was there.
My car, Black782 and the BC2BC car, tested at about 89% of available battery capacity, and drove to 91% of available capacity. That’s within 2% between the two figures and a reasonable error. Other cars had HUGE differences between the instruments and the actual range performance. So, Andy Palmer was right… they have poor instruments. But, he was wrong about the batteries. It was sheer stupidity to tell this group of owners that the batteries are ok. A California study showed that about half the owners have post-graduate degrees, and many of those are in technical fields. A significant percentage have owned electric vehicles prior to the LEAF, and many, if not most of those who have traded their faulty LEAF have gotten another electric powered car, like the GM Volt, and like me, another LEAF.
Nissan – Renault chairman Carlos Ghosn announced Friday that 2013 LEAFs would have a new battery design. One has to wonder if this is merely public relations move to deflect from the current battery woes, or if a real new battery will emerge. Then, we have to wonder if they employed the same testing that the current batteries were exposed to. Nissan really needed to get the LEAF right the first time, and they did an absolutely incredible job overall. I tell everybody know that it’s a fantastic car with one fatal flaw.
I would like to thank everybody who helped make this test a reality, and a fun experience. There are literally dozens who participated. Four of the cars were damaged during loading on the Uhaul rental tow dollies, and many folks have expressed interest in donating money to offset costs and damages from this event. You’re welcome to email me at [email protected] and I will let you know how to send a donation. All monies will first reimburse the owners of damaged cars (I’m not going to fix mine, however, so I don’t need reimbursement), and then any donations above that will go into the non-profit company that I founded to provide electric vehicle charging in California. I won’t personally take any donations.
Tony Williams
Edit: we drove a brand new LEAF, "Red065", on Nov 4, 2012 in Phoenix with only 138 miles on the odometer (and a recent production date) to run the exact course and parameters in similar weather as the Sept 15, 2012 LEAF range autonomy demonstration. This was a shortcoming of our original test, with no "control" car that was capable of producing 84 miles of range autonomy at 4 miles/kWh:
83.2 miles driven (with 21 Gids / 7.47% remaining)
88.7 miles calculated range to turtle
Start battery stored energy: 265 Gids / 94.3%
Start pack volts: 393.5 (4.1 per cell average)
Start SOC: 91.4%
Start GOM: 103
Start temperature: 6 bar segments
Economy: 0 miles/kWh (reset)
Highest cellpair: 4095mv
Lowest cellpair: 4055mv
Average cellpair: 4093mv
Max voltage delta: 40mv (50mv max allowable)
End of test battery stored energy: 21 Gids / 7.47%
TEST COMPLETE. The car was driven an additional 4 miles to a charger when these readings were recorded:
Gids: 11 / 3.9% remaining
Pack volts: 317.5 (3.3 volt average per cell)
SOC: 4.3%
GOM: "---" (normal for "Very Low Battery")
Battery temperature: 7 bar segments
Economy: 4.3 miles/kWh
Subsequent 2013 LEAF-S Range Test on Feb 22, 2013
Subsequent 2012 & 2013 LEAF-SL Range Test, San Diego, March 8, 2013
Nissan LEAF Range Autonomy Demonstration
With Reduced Battery Capacity
September 18, 2012
by
Tony Williams
San Diego, California USA
[email protected]
The Nissan LEAF electric car was introduced to the world as a mass production vehicle during December 2010. Almost 40,000 have been sold around the world in the short time since then, with well over 10,000 sold in the USA. Unfortunately, a percentage of those USA cars that are operated in hot climates, such as Phoenix, Arizona, and the state of Texas, have experienced accelerated losses of the vehicle’s range autonomy, when compared to its performance when new. The phenomenon is not relegated solely to areas of extreme heat; many LEAFs now in moderate temperature areas of California have also experienced significant range autonomy reduction, however not yet to the extent of those cars exposed to Arizona and Texas heat.
When customers have complained, thus far Nissan has claimed that any reduction in range is “normal”, regardless of how much that capacity loss is. Battery issues that are covered under the warranty include “power” to accelerate, or a specific battery failure or abrupt change in the battery performance. Nissan specifically claims that they do not warranty capacity. Nonetheless, in late 2011, Nissan did exchange at least one battery of an Arizona LEAF when its owner complained of reduced capacity. That replacement battery also began degrading recently, and the owner subsequently relinquished the car as a result.
In July 2012, with increasing numbers of LEAFs reporting battery capacity problems, Nissan took approximately one half dozen Phoenix area LEAFs whose owners had complained of reduced range and lowered battery capacity (as indicated by the vehicle’s dash mounted instrument) to its corporate testing facility in Casa Grande, Arizona.
All of those cars have since been returned to their owners, however none of those returned cars had reported any positive change in actual performance by their owners. One car’s battery capacity instrument was reset by Nissan to a “like new” battery indication of 12 of 12 instrument segments, from its previous 10 or 12 segments (10 segments indicates 72.5% - 78.74% battery capacity per Nissan documents). This same car once again lost the 12th capacity segment (with 11 of 12 remaining) on Sunday, September 16, 2012. Of the cars sent to Casa Grande, none have been reported to have been driven by Nissan more than a few dozen miles while at the testing facility.
One prominent Nissan executive is frequently quoted saying that the LEAF should have 80% capacity in 5 years, and 70% capacity in 10 years, and in fact, he specifically states during a Nissan produced YouTube video that those figures are considered “gradual” loss of capacity. Earlier this month, an Australian news agency reported that a Nissan Executive Vice President with specific experience with the LEAF, Mr. Andy Palmer, said that there is “no problem” with the LEAF battery, and that the any customer complaints were merely the result of instrument problems.
In response to this revelation, a group of twelve Nissan LEAFs were independently gathered on Saturday, September 15, 2012 in Phoenix to put this statement to an actual range test; driving a fully charged LEAF in controlled conditions to measure how far they could actually go. Any battery test (or allegation of good batteries) is meaningless if the car can’t actually do the job it was designed to do. In the USA, that job is advertised as traveling “100 miles” (161km), and even further, 200 kilometers (124 miles) in Japan. Clearly, if Nissan truly felt that the batteries were performing as designed for the customer cars they tested at Casa Grande in July, they could have simply verified that at the private, purpose built test track at their disposal there. The actual driving portion of the test would have taken about 90 minutes per car, but they chose not to. Four of the twelve cars in Saturday’s Phoenix area test were previously at the Casa Grande test facility in July.
A staging area was selected at 7755 South Research Drive, Tempe, Arizona, which has one DC Chademo fast charger, and two J1772-2009 EVSE charging stations. Equipment was used to split the latter two stations into four total EVSE’s. This staging site was conveniently located within 0.3 miles (0.5 km) from the main highway. The route traveled was highway 101 north for 5.2 miles (8.3 km), then highway 202 west which becomes highway 10 west. Each car continued west until a predetermined course reversal point, and then returned to near the starting point. This route is largely level and with dry asphalt or concrete roadbed in excellent condition.
Turn around points were determined based on predicted range of each car after considering each car’s battery capacity meter and viewing the car’s report of stored watt-hours with additional equipment. The following round trip distances apply at these course reversal exits on highway 10. The total distance measured is from the staging area and ending on the 101 highway southbound at the East Elliot Road overpass at highway 101. The percentages are the battery’s stored available energy:
62% - 52.3 miles (83.7 km) - Exit 136, 75th Avenue
64% - 54.3 miles (87.4 km) - Exit 135, 83rd Avenue
67% - 56.3 miles (90.6 km) - Exit 134, 91st Avenue
69% - 58.3 miles (93.8 km) - Exit 133a, 99th Avenue
74% - 62.3 miles (100.3km) - Exit 131, 115th Ave / Avondale Boulevard
79% - 66.3 miles (106.7km) - Exit 129, Dysart Road
81% - 68.3 miles (109.9km) - Exit 128, Litchfield Road
85% - 72.3 miles (116.4km) - Exit 126, Pebble Beach Parkway / Estrella Parkway
91% - 76.3 miles (122.8km) - Exit 124, Cotton Lane / highway 303
98% - 82.3 miles (132.5km) - Exit 121, 195th Avenue / Jackrabbit Trail
101%- 85.1 miles (136.9km) - Exit 120, Airport Road / Verrado Way
109%- 91.5 miles (153.0km) - Exit 117, Watson Road
The dash display of Battery Capacities per Nissan documents are as follows:
53.75% - 59.99% - 7 segments of 12 illuminated
60.00% - 66.24% - 8 segments of 12 illuminated
66.25% - 72.49% - 9 segments of 12 illuminated
72.50% - 78.74% - 10 segments of 12 illuminated
78.75% - 84.99% - 11 segments of 12 illuminated
85.00% - 100.0% - 12 segments of 12 illuminated
The backup routes, in case of highway closures, crashes, etc., were either a 40.4 mile (64.6 km) “RIGHT LOOP” consisting of highway 101 North, 60 East, 202 South and then West, then 101 North again, or a 21.8 mile (34.9 km) “LEFT LOOP” via 101 North, 60 West, 10 South, 202 East and returning to 101 North. None of the cars took either of these latter routes. The only highway closure was Cotton Lane exit on highway 10.
The course was driven at 100 km/h as measured by the LEAF’s onboard GPS (62 mph ground speed, 64 mph indicated speed as displayed on the LEAF’s speedometer) with the cruise control engaged. It was estimated that this speed would yield a target energy usage rate of 4 miles (6.437 km) per kWh without climate control. Based on Nissan’s published official range data below (from Nissan Technical Bulletin NTB11-076a), it was determined that a new car would travel 84 miles (135 km) until “turtle” mode (a reduced power mode to safely get the vehicle off the road before the battery disengages power altogether). This data is consistent with extensive publically available independent testing.

Air Density Calculation
Elevation: 1135 feet (346 meters)
Air Temperature: 80F (26.6C)
Altimeter Setting: 30.09 inches Hg (1018.5 hPa)
Dew Point: 43F (6C)
Density Altitude: 2685 feet (819 meters)
Absolute Pressure: 28.864 inches Hg (977.46 hPa)
Air Density: 0.0706 lb/ft3 (1.132 kg/m3)
Relative Density: 92.38%
All LEAFs in this test had the front bumper tow hook installed. All trip odometers, miles/kWh, average speed, timers, etc., were reset. Headlights were on, climate control off and tires set to 36 pounds per square inch (2.48 bars) pressure. All assigned routes were programmed into each navigation display.
Each car had a stored energy display meter (Gidmeter) installed. A new LEAF in optimum condition will show 281 units reported by the LEAF’s automation, for a total of 281 x 80 watt hours per unit = 22.48 kWh stored in the battery. This value, referred to in the LEAF community as “Gids”, is alternately displayed as a percentage of 281 (281 would equal 100%). The LEAF battery has an advertised capacity of 24 kWh.
To help keep track of each of the cars, the last three digits of the LEAF's serial number were affixed on the right top front of the windshield and left rear top of the rear window. Stickers were added to the dash to remind the drivers not to use climate control (or even turn the fan on, as that powers the climate control) and for other safety related functions. Lighter weight driver’s cars had ballast added to match heaviest drivers. The front windows could be either closed, or up to 2 inches open. Rear windows were not to be opened. Most drivers were not the owner of the car they drove, but instead drove another car. Every car was charged the night before, and left outside to be exposed to ambient air for a minimum of 4 hours (most cars well exceeded this). A secondary goal to this was to allow time for the LEAF’s automation to properly balance the 96 cell pairs.
At the start of each car’s test, the driver recorded the starting position GPS coordinates, time from the GPS clock, battery pack voltage (typically 393.5), the “Gid” percentage, Fuel segments observed (in every case, 12), battery capacity segments (varied from 8 to 12, depending on which car) and battery temperature segments displayed (6 in every case, indicating temperatures between approximately 50F (10C) to 100F (38C) per Nissan documents).
Each car had a nine page comprehensive checklist and information package. Finally, the “Distance to Empty” meter readout was recorded. This is largely for entertainment value, as the meters are known to provide such wide variations from actual expected performance that it is affectionately known as the “Guess… Oh… meter”, or “GOM” amongst LEAF owners.
At the conclusion of each run, after the car was safely off the road, and awaiting one of five recovery vehicles used (four rental car dollies attached to gasoline tow vehicles, and one flatbed truck), GPS coordinates were once again recorded, the time from the GPS clock, battery pack voltage, Gid percent, fuel bar segments illuminated, battery capacity segments illuminated and temperature segments illuminated. Finally, the trip odometer mileage and the dash readout of miles/kWh were recorded.
Following is the performance of each car:

*White626 had previous lost one, then two capacity segments. Then, the car was sent to Nissan's test facility at Casa Grande and when it was returned, all 12 capacity segments were restored. One day after this test, it once again lost one capacity segment, now down to 11.
Conclusions and Opinions
The Nissan LEAF has only been on the world stage for about 21 months. Many in the automotive battery world expressed concern over Nissan deploying this chemistry in hot climates without a means to regulate battery temperature long before a single LEAF was built. Only LEAFs in very stable and mostly cool places like England, the San Francisco peninsula, Seattle, Portland (which this summer had unseasonably cooler temperatures, while the rest of the USA baked) have been largely immune from degradation. Even San Diego, where I live, has reported cases of battery degradation.
Both of the 2012 cars (my car was one of them) in the test were replacements for previous LEAFs that suffered battery degradation. Nissan offered no assistance or consideration for the previous cars shortcomings for these new leases. Battery reports issued by the dealers were consistently “5 of 5” stars.
One of the many challenges in this endeavor was finding a “control” car that could actually test out at 100% battery capacity. LEAFs sitting on dealer’s lots in Phoenix, and other hot places, usually with very high states of charge, are in a very difficult situation for the long life of the battery. None of the cars in our group could even come close to 100%, and that includes both of the 2012 model cars, both of which were built in April 2012; one with 2500 and the other 7000 miles.
I planned, and completed a promotional trip from Mexico to Canada, “BC2BC”, in June 2012 with my Nissan LEAF. However, my first car could not complete the trip as planned, due to its reduced range capability, so I leased my current LEAF, built in April 2012 and took delivery at the end of May. Now, with 7000 miles (11000 km), and only 3 months of actual use, this car could not complete the trip that it did in June. During the BC2BC trip, several times I arrived with 4%-5% capacity remaining, which means today, just a few months later, I would come up 4%-5% short. This car has never been exposed to the heat of Phoenix, although it was 104F (40C) in San Jose, California the one day that I was there.
My car, Black782 and the BC2BC car, tested at about 89% of available battery capacity, and drove to 91% of available capacity. That’s within 2% between the two figures and a reasonable error. Other cars had HUGE differences between the instruments and the actual range performance. So, Andy Palmer was right… they have poor instruments. But, he was wrong about the batteries. It was sheer stupidity to tell this group of owners that the batteries are ok. A California study showed that about half the owners have post-graduate degrees, and many of those are in technical fields. A significant percentage have owned electric vehicles prior to the LEAF, and many, if not most of those who have traded their faulty LEAF have gotten another electric powered car, like the GM Volt, and like me, another LEAF.
Nissan – Renault chairman Carlos Ghosn announced Friday that 2013 LEAFs would have a new battery design. One has to wonder if this is merely public relations move to deflect from the current battery woes, or if a real new battery will emerge. Then, we have to wonder if they employed the same testing that the current batteries were exposed to. Nissan really needed to get the LEAF right the first time, and they did an absolutely incredible job overall. I tell everybody know that it’s a fantastic car with one fatal flaw.
I would like to thank everybody who helped make this test a reality, and a fun experience. There are literally dozens who participated. Four of the cars were damaged during loading on the Uhaul rental tow dollies, and many folks have expressed interest in donating money to offset costs and damages from this event. You’re welcome to email me at [email protected] and I will let you know how to send a donation. All monies will first reimburse the owners of damaged cars (I’m not going to fix mine, however, so I don’t need reimbursement), and then any donations above that will go into the non-profit company that I founded to provide electric vehicle charging in California. I won’t personally take any donations.
Tony Williams
Edit: we drove a brand new LEAF, "Red065", on Nov 4, 2012 in Phoenix with only 138 miles on the odometer (and a recent production date) to run the exact course and parameters in similar weather as the Sept 15, 2012 LEAF range autonomy demonstration. This was a shortcoming of our original test, with no "control" car that was capable of producing 84 miles of range autonomy at 4 miles/kWh:
83.2 miles driven (with 21 Gids / 7.47% remaining)
88.7 miles calculated range to turtle
Start battery stored energy: 265 Gids / 94.3%
Start pack volts: 393.5 (4.1 per cell average)
Start SOC: 91.4%
Start GOM: 103
Start temperature: 6 bar segments
Economy: 0 miles/kWh (reset)
Highest cellpair: 4095mv
Lowest cellpair: 4055mv
Average cellpair: 4093mv
Max voltage delta: 40mv (50mv max allowable)
End of test battery stored energy: 21 Gids / 7.47%
TEST COMPLETE. The car was driven an additional 4 miles to a charger when these readings were recorded:
Gids: 11 / 3.9% remaining
Pack volts: 317.5 (3.3 volt average per cell)
SOC: 4.3%
GOM: "---" (normal for "Very Low Battery")
Battery temperature: 7 bar segments
Economy: 4.3 miles/kWh